潮汐力有多可怕,我们拿一个茶壶和茶杯举例子:
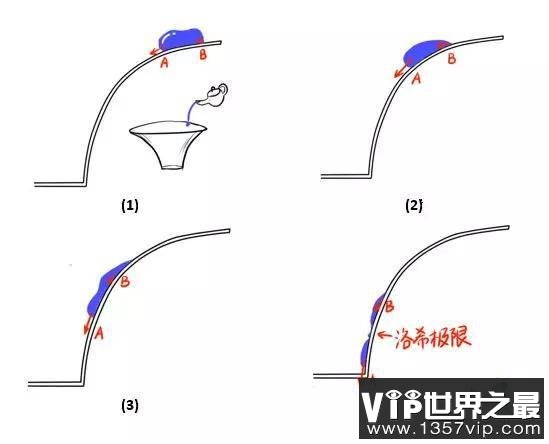
图 c 用来演示潮汐力的茶杯 我们在杯壁顶部倒一些水,让它在重力作用下向着杯底滑落。越靠近杯底,水滴会越拉越长,最后被拉扯到了撕裂的极限。这个极限就可以被认为是这个茶杯对水滴的“洛希极限”。
木星的引力场,实际上就是这样一个“茶杯”。地球尺寸很大,当它靠近木星时,离木星较近一侧受到的引力,将比较远一侧大得多,因此会像水滴一样被逐渐撕裂。
“洛希极限”究竟是什么?
卫星绕着中心天体旋转需要“向心力”,通常由两者之间的万有引力提供。当卫星旋转角速度固定时,“向心力”和旋转半径成正比,但是万有引力和旋转半径的平方成反比。两者变化正好相反,导致卫星内部受力不均匀。在卫星靠近中心天体的一侧,向心力小于万有引力;在背离中心天体的一侧,向心力大于万有引力。
现在,我们借助“两个铁球同时落地”的思想,把卫星看成铁链拴住的两个铁球。对于靠近中心天体的铁球,万有引力提供向心力还有多余;另一个铁球,万有引力无法提供足够的向心力。这事,中间的铁链正好“损有余而补不足”,通过传递作用力,使“卫星”在整体上处于受力平衡的状态。

铁链是有一定强度的,传递的力量过大就会断裂。而且,这是没有考虑卫星自转的情况,如果卫星自转,铁链还要加上自转产生的离心力。这个刚好使“铁链”断裂的距离,就是卫星对中心天体的“洛希极限”。

洛希极限公式
木星密度:1.326g/cm3
地球密度:5.516g/cm3
对于一个完全刚体、圆球形的卫星,假设其物质都是因为重力才合在一起的,且所环绕的行星亦是圆球形,并忽略其他因素如潮汐变形及自转。
其中R是卫星所环绕的星体的半径,ρM是该星体的密度,ρm是卫星的密度。
对于是流体的卫星,潮汐力会拉长它,令它变得更易碎裂。

由于有黏度、摩擦力、化学链等影响,大部分卫星都不是完全流体或刚体,其洛希极限都在这两个界限之间。
如果一个刚体卫星的密度是所环绕的星体的密度两倍以上(例如一个巨大的气体行星跟刚体卫星;对于流体卫星来说,则要约14.2倍以上),d < R,洛希极限会在所环绕的星体之内,即是说这个卫星永远都不会因为所环绕的星体的引力而碎裂。
这是一个理想状况下的静态洛希极限式,只有在实验室里摆置两个星球才会出现这种情况。
19世纪,法国天文学家爱德华·洛希经过研究计算后,他发现当两个天体的距离不断接近,并且接近到一个极限值的时候,其中一个天体可能就会被另一个天体施加的潮汐力撕碎。后来,人们把这个极限被称为“洛希极限”。
“洛希极限”提到。假定,两个天体之间的质量差距非常大,那么洛希极限的值只与两个天体的密度与被撕碎物体的物理状态有关,将大天体密度与小天体的密度的比值开3次方后,再乘以大天体的半径以及一个倍数,就是洛希极限的值。
洛希极限又分为流体洛希极限和刚体洛希极限,如果被撕碎物体为气体、液体或者非常松散的固体,这个倍数就是2.455;如果被撕碎物体是很坚硬的固体,这个倍数就是1.26。后者即为电影中提到的刚体洛希极限。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

